Exploring the Transformer’s Decoder Architecture: Masked Multi-Head Attention, Encoder-Decoder Attention, and Practical Implementation
This article was co-authored by Luís Roque and Rafael Nardi
Introduction
In this article, we delve into the decoder component of the transformer architecture, focusing on its differences and similarities with the encoder. The decoder’s unique feature is its loop-like, iterative nature, which contrasts with the encoder’s linear processing. Central to the decoder are two modified forms of the attention mechanism: masked multi-head attention and encoder-decoder multi-head attention.
The masked multi-head attention in the decoder ensures sequential processing of tokens, a method that prevents each generated token from being influenced by subsequent tokens. This masking is important for maintaining the order and coherence of the generated data. The interaction between the decoder’s output (from masked attention) and the encoder’s output is highlighted in the encoder-decoder attention. This last step gives the input context into the decoder’s process.
We will also demonstrate how these concepts are implemented using Python and NumPy. We have created a simple example of translating a sentence from English to Portuguese. This practical approach will help illustrate the inner workings of the decoder in a transformer model and provide a clearer understanding of its role in Large Language Models (LLMs).
As always, the code is available on our GitHub.
One Big While Loop
After describing the inner workings of the encoder in transformer architecture in our previous article, we shall see the next segment, the decoder part. When comparing the two parts of the transformer we believe it is instructive to emphasize the main similarities and differences. The attention mechanism is the core of both. Specifically, it occurs in two places at the decoder. They both have important modifications compared to the simplest version present at the encoder: masked multi-head attention and encoder-decoder multi-head attention. Talking about differences, we point out the recurrent aspect of the decoder contrasting with the linear encoder. The decoder is a big while loop.
The self-attention mechanism performs the computation of relations between words/tokens using a (scaled) inner product of vector representations Q and K of these tokens, that, upon training, capture the probability these words have to appear in the same sentence. These scalar products form a matrix of weights that multiply by another representation V of the same tokens. Hence, the vectors V are updated by the weights through simple matrix multiplication in such a way that every vector in the stack of V receives the information coming from every other vector in the stacks of Q and K. This encompasses the core idea coming from linguistics that “You shall know a word by the company it keeps” attributed to John Rupert Firth. More formally, we have:
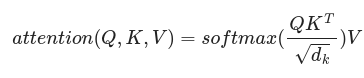
But now, in the decoder part, we want the algorithm to create one token each time only considering the previous ones already generated. To make this work properly, we need to forbid the tokens from getting information from the right of the sentence. This is done by masking the matrix of weights so that it ends up being of triangular shape, having zeros for all its components above the diagonal. Thus, we write:
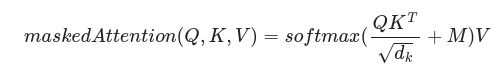
where M is the mask matrix with components above the diagonal, which produces zeros under exponentiation in softmax. The stack of vectors V gets updated in such a way that the first in the V-stack gets information only from itself, the second gets information from itself and the previous one, and so on.
The other instance where the attention mechanism takes place in the decoder segment is the so-called encoder-decoder attention. The basic difference is that the Q vector is the output of the masked attention (after the residual connection) while K and V vectors come from the encoder part.
This gets clearer when we consider the main difference between the encoder and decoder parts of the transformer, as we mentioned before: the while-loop characteristic of the decoder.
The user does not control the input of the masked attention layer. Instead, it is constituted by the vectors previously generated in their own loop starting with a special token <START> and ending with another special token that indicates the end of the sentence: <EOS>. There is a caveat that we need to cover here. If this process worked completely on its own, it would have no source of information from the user at all, and therefore, the task of translation would be impossible. So, the encoder-decoder attention bridges the embeddings K and V from the encoder, which carries the original information one wants to process, and the Q vectors, which are generated in the decoder loop.
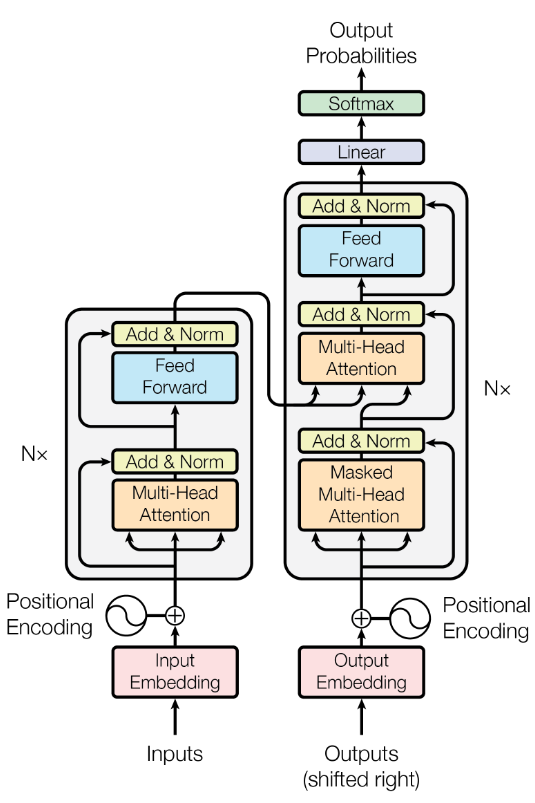
Also, it is worth noticing that it is here where one can capture the motivation for the names of these sets of vectors: the Q vectors generated in the loop work like true Queries (since they find a match for those tokens already generated in the loop) that are paired with the K (Key) vectors through scalar products and produce a result, the updated V (Value) vectors.
Follow the Numbers
In the following, we consider the same sentence we used in our previous article, now feeding the decoder to perform a translation task to the Portuguese language.
As we saw, the encoder takes the initial embedding X of the sentence ‘Today is sunday’. This time we use a 5-dimensional initial embedding (for reasons that will be clear soon):
‘Today’ — (1,0,0,0,0)
‘is’ — (0,1,0,0,0)
‘sunday’ — (0,0,1,0,0)
from a total of 4 tokens in our dictionary, which also have
‘saturday’ — (0,0,0,1,0).
So, the input of the encoder is:
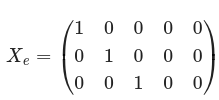
X_e is mapped to the 3 sets of vectors, Q, K, and V, by means of matrix multiplication:

where W matrices are randomly initiated and adjusted along training. Also, we added the subscript e for the encoder. Multi-head attention results in V_e^{updated}.
For the decoder part, we keep the stacks of vectors and V_e^{updated}:

As we mentioned, the decoder works iteratively from a <START> token that we chose to be as follows:

This will be the input of the masked attention after positional encoding:

In the masked attention sector, other 3 sets of vectors are generated, now named Q_m, K_m, and V_m, from 3 other matrices W^m made out of learnable parameters, randomly initiated:

Which, results in the 3 vectors:

The attention score matrix is calculated. In this case, it happens to be just one number:

It is then added to the masking matrix (which is just the number 0) and then scaled through division by the square root of the dimension of Q and K (in this case d_k=5):

For the first iteration, applying the softmax function always results in 1. This works as a weight for the V_m vector:
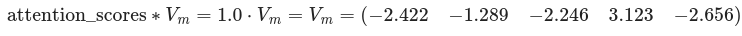
The result of this computation is one single vector V_e^{updated} that then undergoes residual connection:
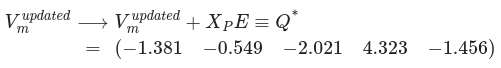
We can implement it using Python using only NumPy in the following way:
class One_Head_Masked_Attention:
def __init__(self, d_model, d_k, d_v):
self.d_model = d_model
self.W_mat = W_matrices(self.d_model, d_k, d_v)
def compute_QKV(self, X):
self.Q = np.matmul(X, self.W_mat.W_Q)
self.K = np.matmul(X, self.W_mat.W_K)
self.V = np.matmul(X, self.W_mat.W_V)
def print_QKV(self):
print(‘Q : \\n’, self.Q)
print(‘K : \\n’, self.K)
print(‘V : \\n’, self.V)
def compute_1_head_masked_attention(self):
Attention_scores = np.matmul(self.Q, np.transpose(self.K))
# print(‘Attention_scores before normalization : \\n’, Attention_scores)
if Attention_scores.ndim > 1:
M = np.zeros(Attention_scores.shape)
for i in range(Attention_scores.shape[0]):
for j in range(i+1, Attention_scores.shape[1]):
M[i,j] = -np.inf
else:
M = 0
Attention_scores += M
# print(‘Attention_scores after masking : \\n’, Attention_scores)
Attention_scores = Attention_scores / np.sqrt(self.d_model)
# print(‘Attention scores after Renormalization: \\n ‘, Attention_scores)
if Attention_scores.ndim > 2:
Softmax_Attention_Matrix = np.apply_along_axis(lambda x: np.exp(x) / np.sum(np.exp(x)), 1, Attention_scores)
else:
Softmax_Attention_Matrix = np.exp(Attention_scores) / np.sum(np.exp(Attention_scores))
# print(‘result after softmax: \\n’, Softmax_Attention_Matrix)
if Attention_scores.ndim > 1:
if Softmax_Attention_Matrix.shape[1] != self.V.shape[0]:
raise ValueError(“Incompatible shapes!”)
result = np.matmul(Softmax_Attention_Matrix, self.V)
else:
result = Softmax_Attention_Matrix * self.V
# result = np.matmul(Softmax_Attention_Matrix, self.V)
# print(‘softmax result multiplied by V: \\n’, result)
return result
def backpropagate(self):
# do smth to update W_mat
pass
class Multi_Head_Masked_Attention:
def __init__(self, n_heads, d_model, d_k, d_v):
self.d_model = d_model
self.n_heads = n_heads
self.d_k = d_k
self.d_v = d_v
self.d_concat = self.d_v*self.n_heads
self.W_0 = np.random.uniform(-1, 1, size=(self.d_concat, self.d_v))
self.heads = []
i = 0
while i < self.n_heads:
self.heads.append(One_Head_Masked_Attention(d_model=d_model, d_k=d_k , d_v=d_v ))
i += 1
def print_W_0(self):
print(‘W_0 : \\n’, self.W_0)
def print_QKV_each_head(self):
i = 0
while i < self.n_heads:
print(f’Head {i}: \\n’)
self.heads[i].print_QKV()
i += 1
def print_W_matrices_each_head(self):
i = 0
while i < self.n_heads:
print(f’Head {i}: \\n’)
self.heads[i].W_mat.print_W_matrices()
i += 1
def compute(self, X):
self.heads_results = []
for head in self.heads:
head.compute_QKV(X)
self.heads_results.append(head.compute_1_head_masked_attention())
if X.ndim > 1:
multi_head_results = np.concatenate(self.heads_results, axis=1)
V_updated = np.matmul(multi_head_results, self.W_0)
else:
multi_head_results = np.concatenate(self.heads_results, axis=0)
print(‘Dimension of multihead_results:’, multi_head_results.shape)
print(‘Dimension of W_0:’, self.W_0.shape)
V_updated = np.matmul(multi_head_results, self.W_0)
return V_updated
def back_propagate(self):
# backpropagate W_0
# call _backprop for each head
pass
Now, we are ready to tackle the next section, the encoder-decoder attention:

Again, we start computing the attention scores, which now form a 1×3 matrix:

We apply the scaling and softmax:

And finally, we get the updated V-vector V*:

Once again, we can implement the above using NumPy:
class One_Head_Encoder_Decoder_Attention:
def __init__(self, d_k):
self.d_k = d_k
def print_QKV(self):
print(‘Q : \\n’, self.Q)
print(‘K : \\n’, self.K)
print(‘V : \\n’, self.V)
def compute_1_head_attention(self, Q, K, V):
self.Q = Q #from masked attention in decoder
self.K = K #from encoder
self.V = V #final result from encoder
Attention_scores = np.matmul(self.Q, np.transpose(self.K))
# print(‘Attention_scores before normalization : \\n’, Attention_scores)
Attention_scores = Attention_scores / np.sqrt(self.d_k)
# print(‘Attention scores after Renormalization: \\n ‘, Attention_scores)
Softmax_Attention_Matrix = np.exp(Attention_scores – np.max(Attention_scores, axis=-1, keepdims=True))
Softmax_Attention_Matrix /= np.sum(Softmax_Attention_Matrix, axis=-1, keepdims=True)
# print(‘result after softmax: \\n’, Softmax_Attention_Matrix)
if Softmax_Attention_Matrix.ndim > 1:
if Softmax_Attention_Matrix.shape[1] != self.V.shape[0]:
raise ValueError(“Incompatible shapes!”)
result = np.matmul(Softmax_Attention_Matrix, self.V)
return result
This last step provides the information associated with the semantic relations in the sentence “Today is Sunday” with the decoder loop. The result V* undergoes another instance of residual connection.

The next segment is the final feed-forward network (FFN). The original paper is made out of 2 matrices of learnable parameters. It is then followed by another instance of softmax that maps to a probability distribution in a space where the identification of tokens in Portuguese takes place through one-hot encoding. This means that if the result of softmax(FFN(RC)) is

then, the associated token will be:

Using the Portuguese vocabulary, we would get:
vocabulary = { 'Hoje': np.array([1,0,0,0,0]),
'é': np.array([0,1,0,0,0]),
'domingo': np.array([0,0,1,0,0]),
'sábado': np.array([0,0,0,1,0]),
'EOS': np.array([0,0,0,0,1]),
'START' : np.array([0.2,0.2,0.2,0.2,0.2])
}
Thus, our token is the following:

Considering the sentence in our example, the expected result would be ‘Hoje’ (the translation of ‘Today’ to Portuguese). Recall that we did not train our model yet (there is no backpropagation).
This is the end of the decoder loop. Now the output is used to feed the loop again appending the previous X = <START> with the vector associated with ‘sábado’, say (0,0,0,1,0), in the Portuguese embedding space.

Notice that two tokens will be generated in this next round instead of one. This number is added by one at each iteration and the model goes on appending the last generated token to the previous until a token is identified with <EOS>.
Zooming in the Masked Attention Layer
To better understand the masked attention, it is instructive to look at what happens when the matrix size is a bit bigger than just one number. We take the third step considering that at the first two, the following tokens were generated:
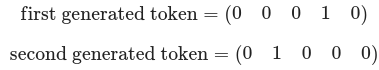
This means that now, the input of the masked attention sector is made out of the stacking of them with older ones at the top and later ones at the bottom of the stack (since we chose to work with -inf above the diagonal in the mask matrix) starting with the <START> token:

This goes through positional encoding,

and results into the Q, K, and V stacks:
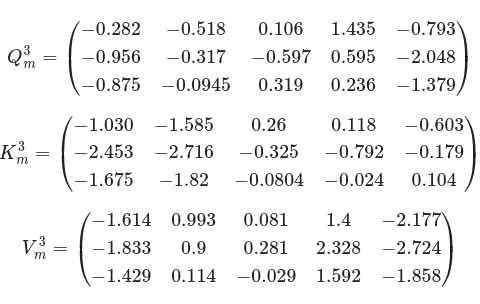
The attention score matrix is:

and the mask M matrix is:

The sum of them is:

which after scaling assumes the following form:

and now goes through softmax:

We finally multiply it by the V-vectors to get the V³_updated:

Here, we can see that the first vector/row didn’t change. Recall that it results from multiplying the first row of softmax(Scaled_Masked_Attention_Scores)³ by all the columns in the V stack. But since this row has zeros for all components other than the first component where it is 1, this first vector in the stack gets contribution coming only from itself multiplied by a weight equal to 1.
The second updated vector gets contributions from the first and second vectors with weights summing up to 1. Analogously, the third updated V-vector gets weighted contributions from itself and the two previous vectors in the V-stack.
We stress the importance of applying the softmax function separately in each row of the masked attention-scaled scores to distribute the weights properly.
We can run the complete process for 10 iterations or until we find an EOS token:
ENDCOLOR = '\\033[0m'
RED = '\\033[91m'
GREEN = '\\033[92m'
BLUE = '\\033[94m'
# encoder constructs the K and V vectors. Lets say we have 3
# five-dimensional vectors for each stack.
K = np.random.uniform(low=-1, high=1, size=(3, 5))
V = np.random.uniform(low=-1, high=1, size=(3, 5))
vocabulary = { ‘Hoje’: np.array([1,0,0,0,0]),
‘é’: np.array([0,1,0,0,0]),
‘domingo’: np.array([0,0,1,0,0]),
‘sábado’: np.array([0,0,0,1,0]),
‘EOS’: np.array([0,0,0,0,1]),
‘START’ : np.array([0.2,0.2,0.2,0.2,0.2])
}
START = vocabulary[‘START’]
EOS = vocabulary[‘EOS’]
INPUT_TOKEN = START
OUTPUT_TOKENS = START
LAST_TOKEN = START
X = INPUT_TOKEN
PE = Positional_Encoding()
multi_head_masked_attention = Multi_Head_Masked_Attention(n_heads=8, d_model=5, d_k=4, d_v=5)
encoder_decoder_attention = One_Head_Encoder_Decoder_Attention(d_k=4)
ffn = FFN(d_v=5, layer_sz=8, d_output=5)
count = 0
while (not np.array_equal(LAST_TOKEN, EOS)) and (count < 10):
X_PE = PE.compute(X)
print(BLUE + ‘shape of X:’, X.shape, ENDCOLOR)
print(BLUE+‘X:\\n’, X, ENDCOLOR)
print(BLUE+‘X_PE:\\n’, X_PE, ENDCOLOR)
output_masked_attention = multi_head_masked_attention.compute(X_PE)
Q_star = add_and_norm(output_masked_attention, X_PE) #residual_connection_1
output_encoder_decoder_attention = encoder_decoder_attention.compute_1_head_attention(Q=Q_star, K=K, V=V)
Rc2 = add_and_norm(output_encoder_decoder_attention , Q_star) # residual connection 2
ffn_result = ffn.compute(Rc2)
OUTPUT_TOKENS_before_softmax = add_and_norm(ffn_result, Rc2) # ——-> 3rd residual connection 3
if OUTPUT_TOKENS_before_softmax.ndim == 1:
# last softmax:
OUTPUT_TOKENS = np.exp(OUTPUT_TOKENS_before_softmax) / np.sum(np.exp(OUTPUT_TOKENS_before_softmax))
position_of_max = np.argmax(OUTPUT_TOKENS)
OUTPUT_TOKENS = np.eye(OUTPUT_TOKENS.shape[0])[position_of_max]
LAST_TOKEN = OUTPUT_TOKENS
else:
OUTPUT_TOKENS = np.apply_along_axis(lambda x: np.exp(x) / np.sum(np.exp(x)), 1, OUTPUT_TOKENS_before_softmax)
position_of_max = np.argmax(OUTPUT_TOKENS, axis=1)
OUTPUT_TOKENS = np.eye(OUTPUT_TOKENS.shape[1])[position_of_max]
LAST_TOKEN = OUTPUT_TOKENS[-1,:]
X = np.vstack([X, LAST_TOKEN])
print(‘shape of OUTPUT_TOKENS:’, OUTPUT_TOKENS.shape)
print(RED+‘OUTPUT_TOKENS:\\n’, OUTPUT_TOKENS, ENDCOLOR)
print(RED+‘LAST_TOKEN:\\n’, LAST_TOKEN, ENDCOLOR)
print(RED + ‘=====================================’ + ENDCOLOR)
count = count + 1
#identifying tokens in dictionary:
OUTPUT_SENTENCE = []
output_sentence_str = ”
for token_pos in range(len(X[:,0])):
token = X[token_pos,:]
for name, array in vocabulary.items():
if np.array_equal(array, token):
OUTPUT_SENTENCE.append(name)
for token_name in OUTPUT_SENTENCE:
output_sentence_str += token_name + ‘ ‘
print(output_sentence_str)
From the above, we got the following output:
<START> domingo Hoje domingo domingo é Hoje domingo domingo Hoje domingoRecall, once again, that our Neural Network with the transformer architecture is not trained, so the weights are just the initial random weights.
Conclusions
Our detailed examination of the transformer architecture’s decoder component shows its intricacies and how it can integrate components from the encoder while generating new information. The decoder’s iterative, loop-based design, is one of the main factors differentiating it from the encoder.
A key innovation is the masked multi-head attention mechanism, ensuring no data leakage in the recursive process. It allows the decoder to process each token independently, which is necessary for tasks like translation. This design mirrors human sentence construction, considering context up to each point in a sequence. Then, the encoder-decoder attention mechanism integrates contextual understanding from the encoder into the decoder’s output. This is the layer that ensures that both components are integrated.
Our practical implementation using Python and NumPy shows how the decoder processes data when performing machine translation.
References
[1] Ashish Vaswani et al. (2017), Attention is all you need https://doi.org/10.48550/arXiv.1706.03762
—
All images are by the author unless noted otherwise.
More articles: https://zaai.ai/lab/co-

